Unity Vector3.Dot, what?

This is the first installment of “stuff I wrote before but I really want to have on my own website”. I wrote this in 2020 and I still find it useful to refresh my memory every now and then.

The Vector3.Dot() function returns the dot product of two vectors. “What?” you might be asking yourself. Let’s take a look at the wikipedia description:

In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number.

Aaah! Okay… What?

Here’s my understanding of what the dot product is:

The dot product is the sum of the axis from two vectors multiplied by each other and can be used to find out where two points are facing relative to each other.

Examples

Let’s look at some vectors and their respective dot products:

• Vectors (3, 2) and (2, 4): 32 + 24 = 14.
• Vectors (-3, 2) and (2, 1): -32 + 21 = -4.
• Vectors (3, 0) and (0, 4): 30 + 04 = 0.

This would work the same with vectors that hold more than 2 values, you just sum three multiplied values instead of two.

Oh okay. So why?

One of the applications for this is to find out if a point is in front of or behind another point. You could for instance figure out if an object is in front of or behind your character.

If you look at the examples again you’ll see the values 14, -4 and 0. The dot product correlates to the relative position the two vectors have to each other. To make it easier to understand I’ve whipped up these dank images:

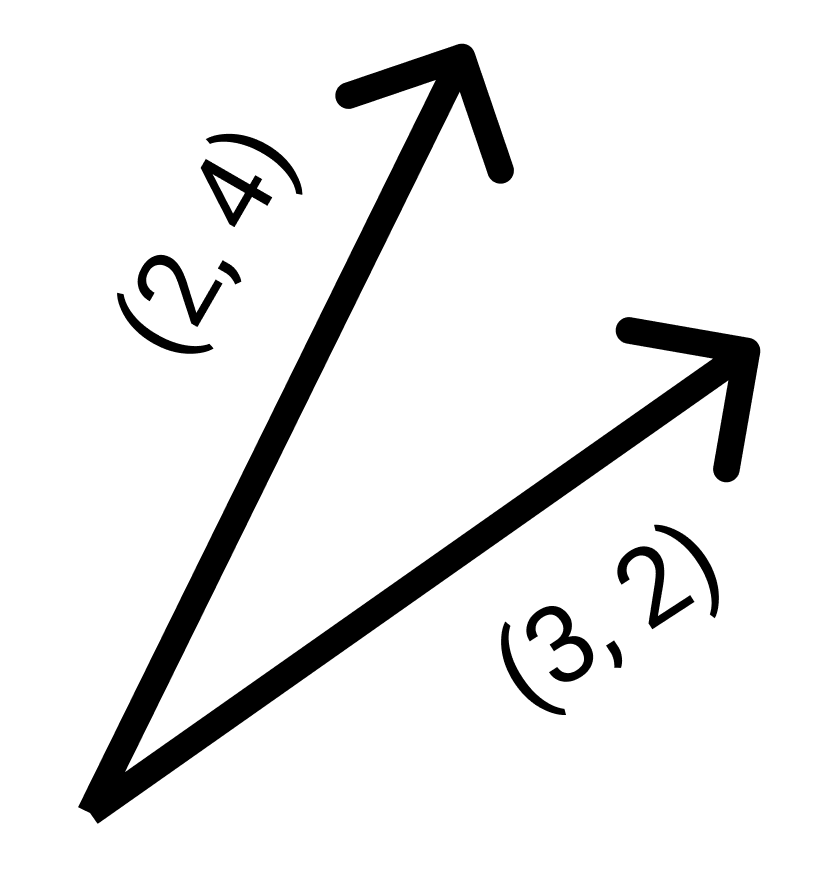
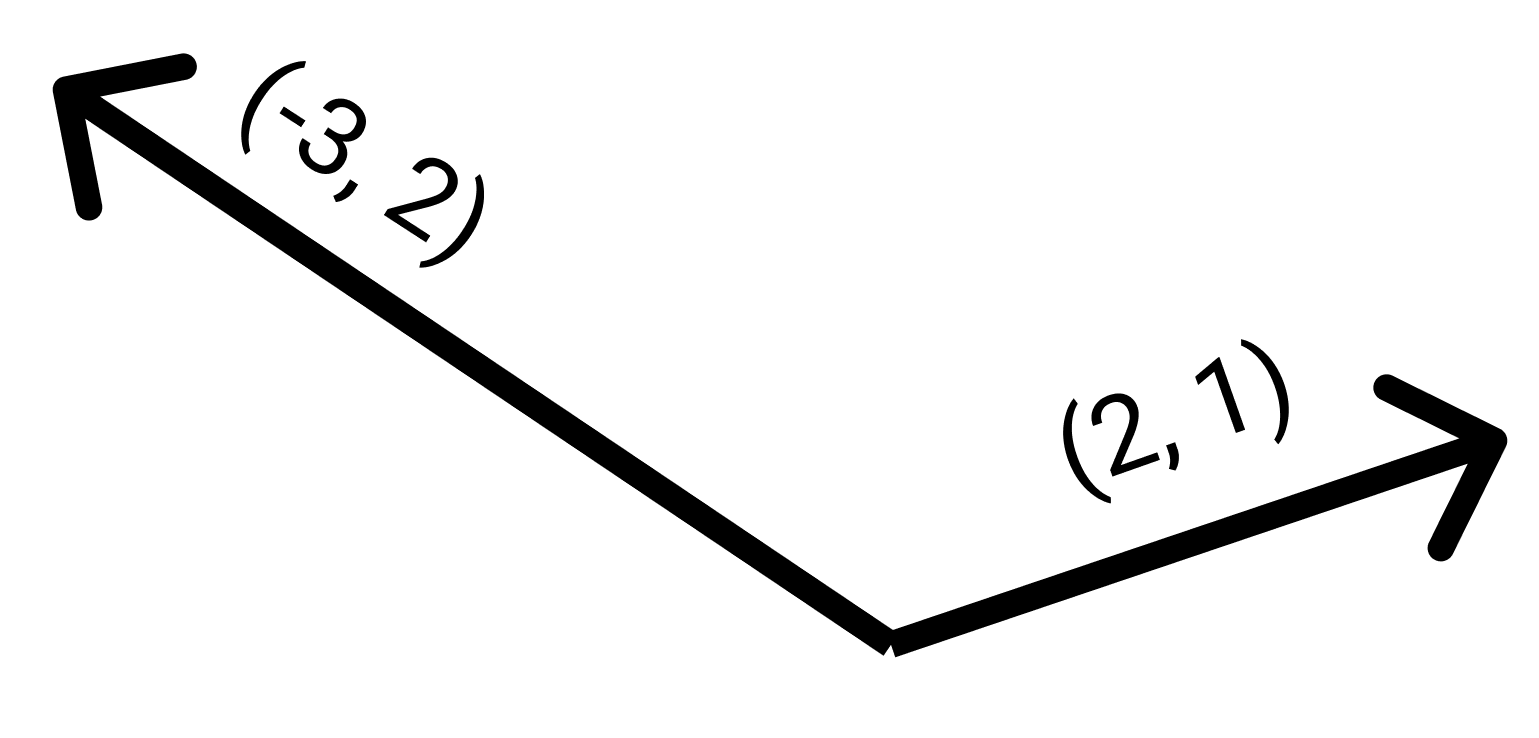
From first to last, the dot products for these vectors are 14, -4 and 0 respectively. A positive value (14) shows us that the vectors are facing the same way as is illustrated by the image. A negative value tells us they’re facing near opposite directions and a 0 value tells us they’re perpendicular to each other.

This is a very fast calculation to perform allowing for a quick direction check, which comes in handy at 60+ fps.

All right. Pretty dumb but whatever

Sssshhh… You can also use the dot product to calculate the angle between an object and the way your character is facing for example. Cool right?

The formula for this is: acos(x · y / ‖x‖ * ‖y‖)

Which is just fancy writing for inverse cosine of dot product of x and y divided by magnitude of x times magnitude of y.

Keep in mind that this is radians though. So… You know, don’t forget to multiply by 180 / pi.

Conclusion

In the end there never is a conclusion.